画像 四 角柱 の 体積 の 求め 方 324439

６年算数 円柱と角柱の体積 教え方２

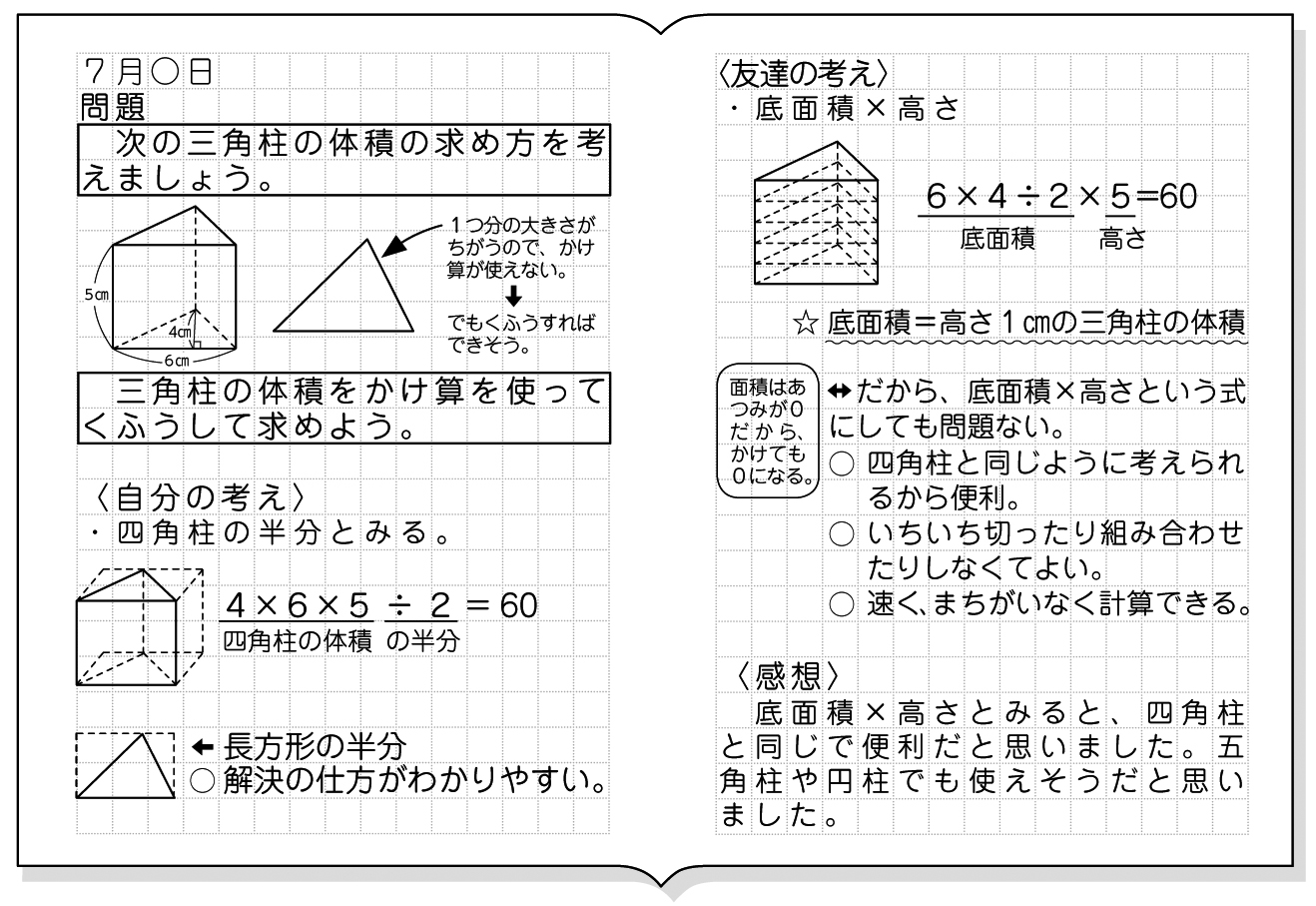
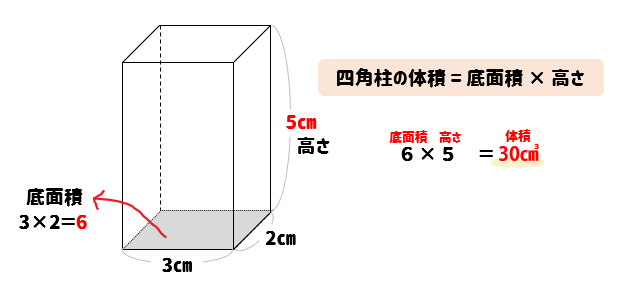
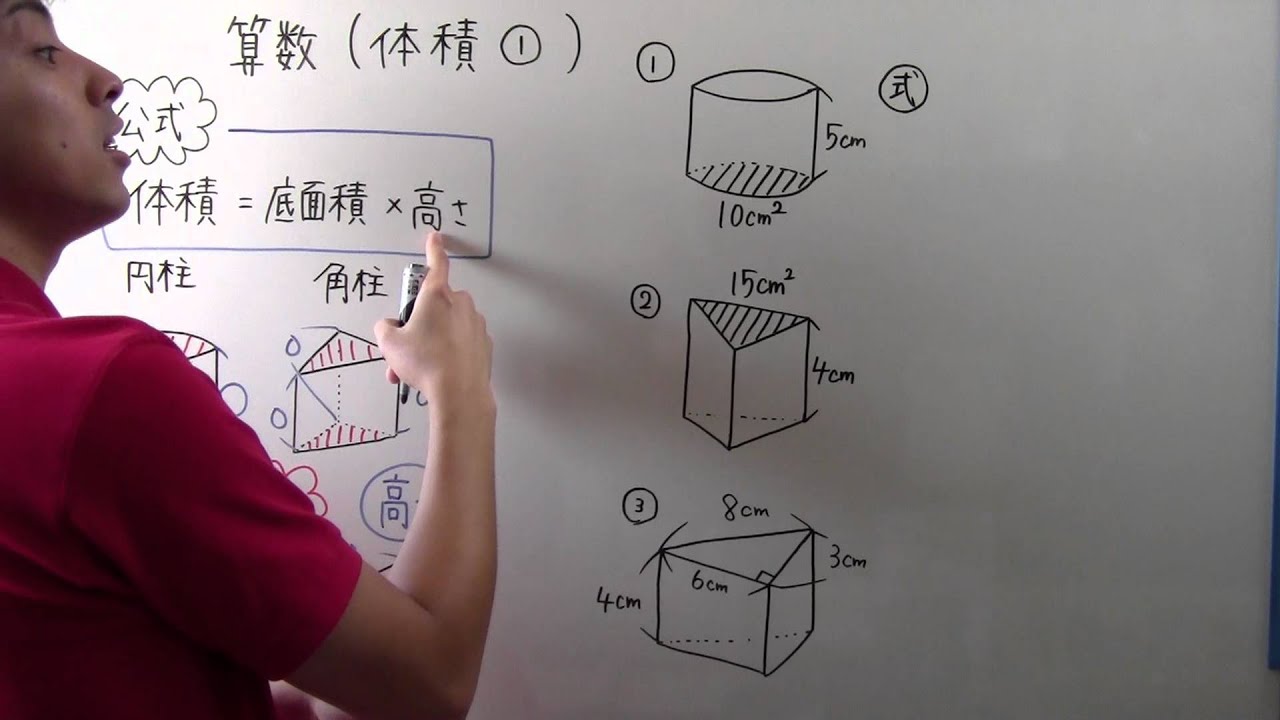
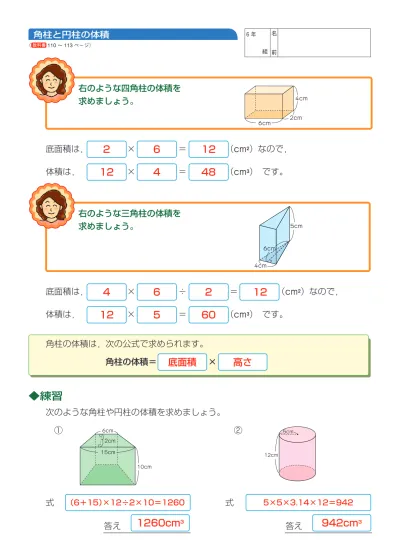
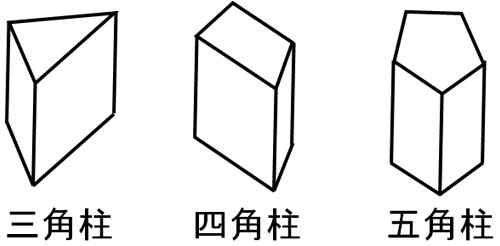
 5年生の角柱の基本事項も復習しておきましょう。 角柱の体積は 底面積×高さ で求めることができます。 三角柱、四角柱、円柱の体積の求め方 三角柱の体積、四角柱の体積、円柱の体積は全て底面積×高さで計算できます。三角柱や四角柱などの体積は、底面積 S S 、高さ h h として、次の式で求められます。 角柱 かくちゅう の体積 V = Sh V = S h 体積 = 底面積 × 高さ 円柱の体積 半径 r、高さ h の 円柱 えんちゅう 円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。 円柱 えんちゅう の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 ×

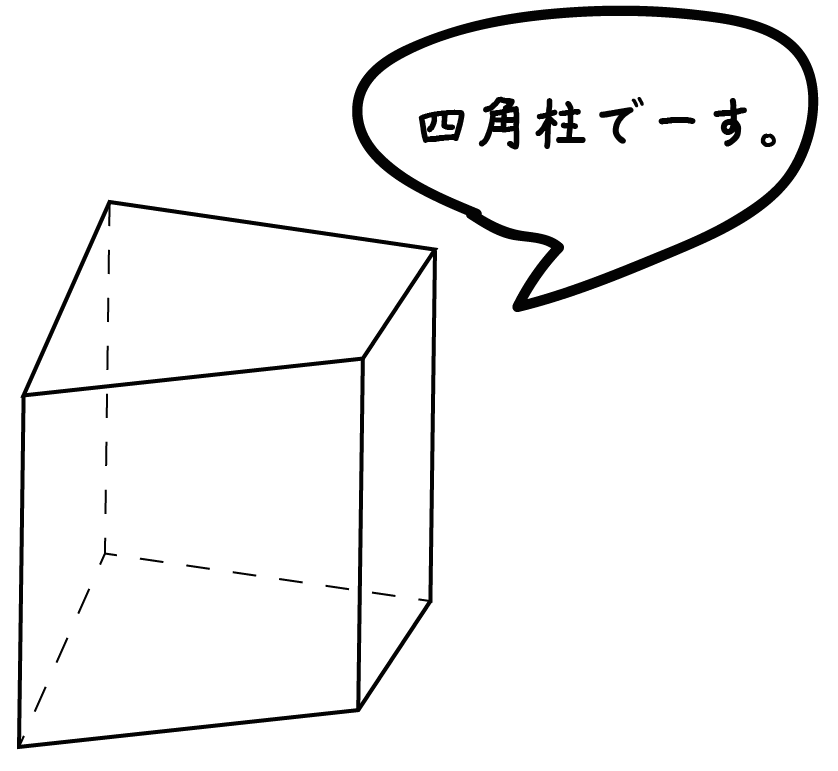
四 角柱 の 体積 の 求め 方

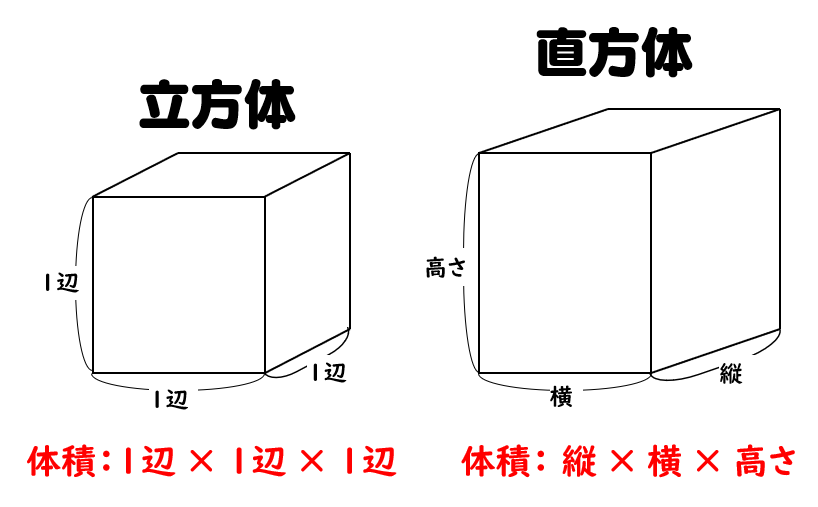
四 角柱 の 体積 の 求め 方- 立体の体積の求め方（公式）を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle柱の体積は，どうやって求めるの （底面が台形） 無断複製・転載・翻訳を禁ず ©GAKKEN B

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

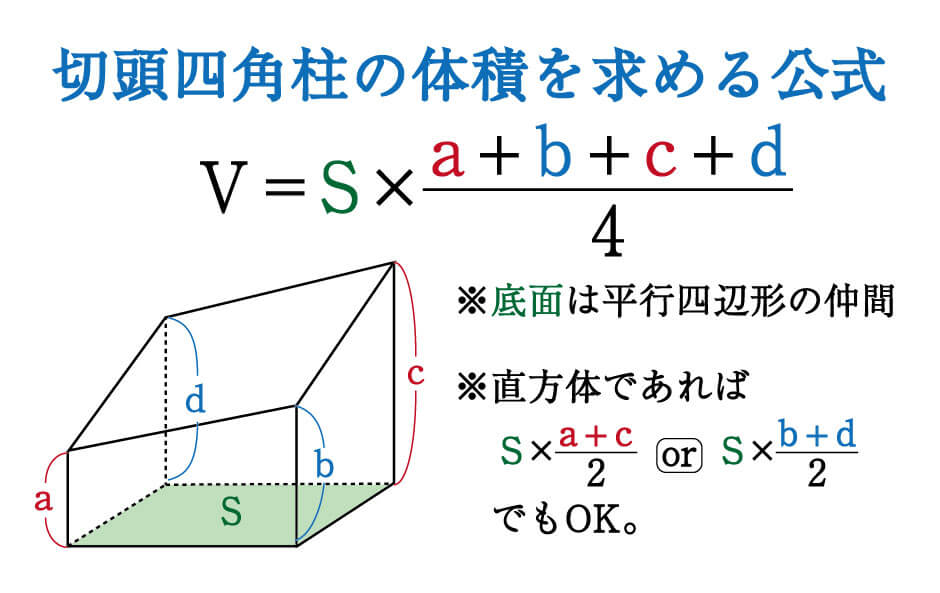
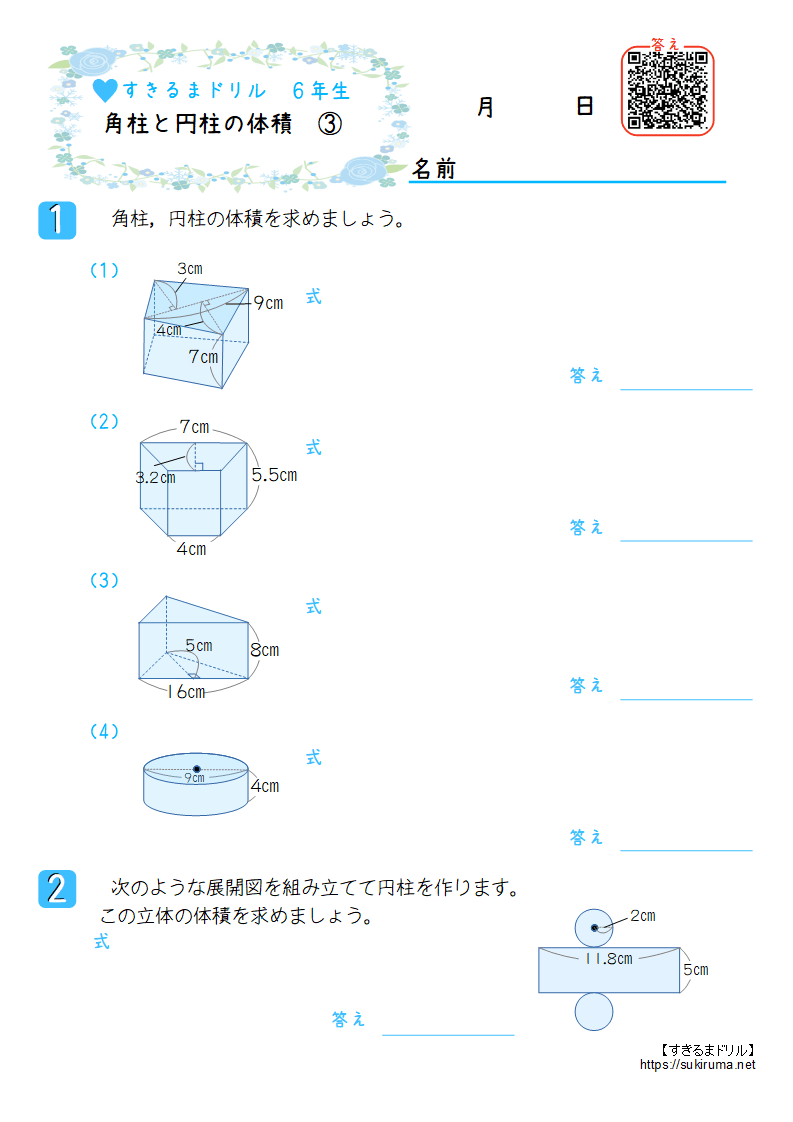
 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、 {（下の辺）×（下の辺） （下の辺）×（上の辺） (上の辺) × (上の辺) }×高さ÷3 ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 2つの円錐の共通部分の体積 8 空間図形と立体図形の違い 9 中3数学の問題です。 二等辺三 10 球と円柱の共通部分の体積 11 1リットルは 何 立方ミリメ 12 円周率の2乗 13 n次元の体積の求め方 14 図のような立方体125個でできた 15 錐の体積 16 角柱の体積の求め方 に 円錐や角錐の体積をもとめる時に、なぜ3分の1をかけるのか教えていただけませんか。 補足日時： 2304 あの方法で、立方体は3個の合同な四

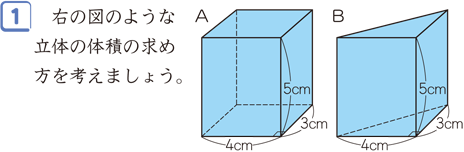
 積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない（円錐でも三角錐でも四角錐でも適用可能）証明方法です。 《四角錐の体積の求め方》 （底面は一辺が5cmの正方形） 四角錐の体積＝底面積×高さ× 1 3 なので 求める四角錐の体積＝5×5×15× 1 3 ＝125（cm³） 答え 125cm³ スポンサードリンク 問題② 次の四角錐の体積を求めましょう。 《四角錐の体積の求め方》 四角錐の体積＝底面積×高さ× 1 3 なので 求める四角錐の体積＝36×8× 1 3 ＝96（cm³） 答え 96cm³ 問題③ 次の四角錐の高さを求角柱の体積基本 目標時間 名前 次の立体の体積の求め方を考えましょう。 ① 次の直方体の体積を求めましょう。 式 答え 直方体の体積は 縦 × 横 × 高さ で求められます。 ② の部分を底面積といいます。 底面積を求めましょう。 式 答え ③ ②で求めた底

四 角柱 の 体積 の 求め 方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	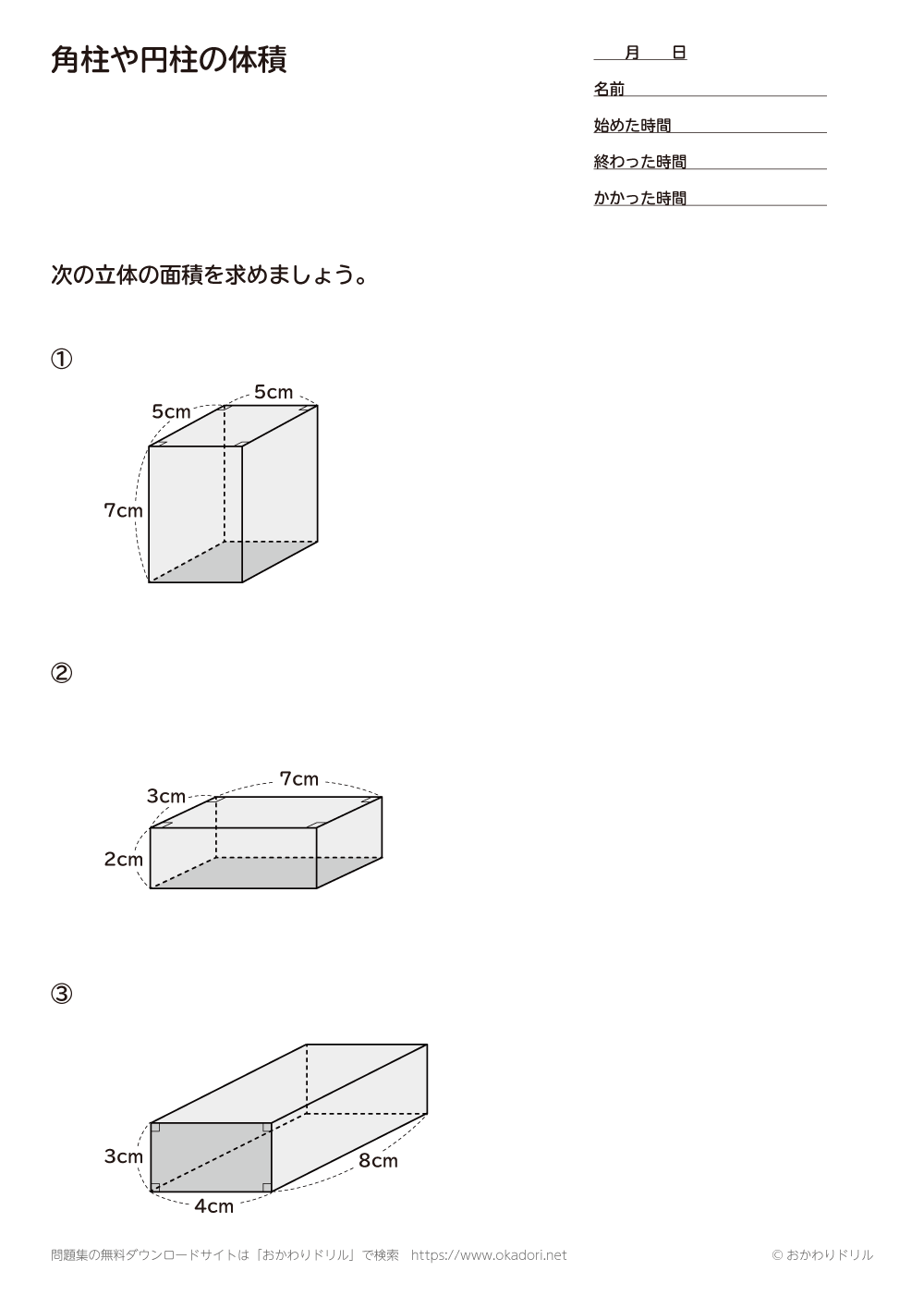立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	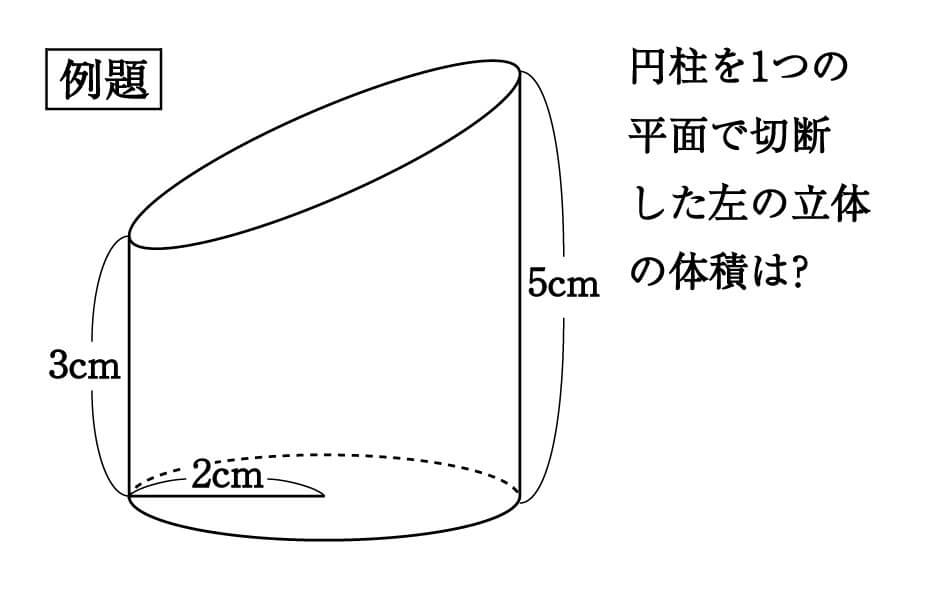立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	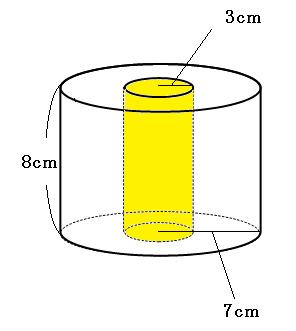立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	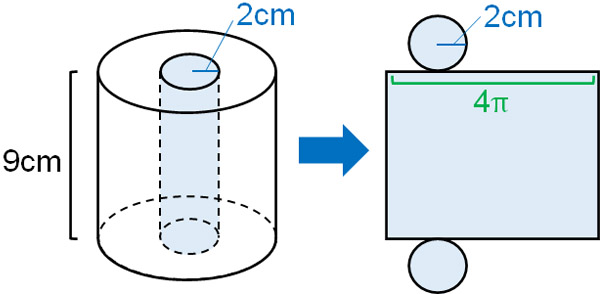立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
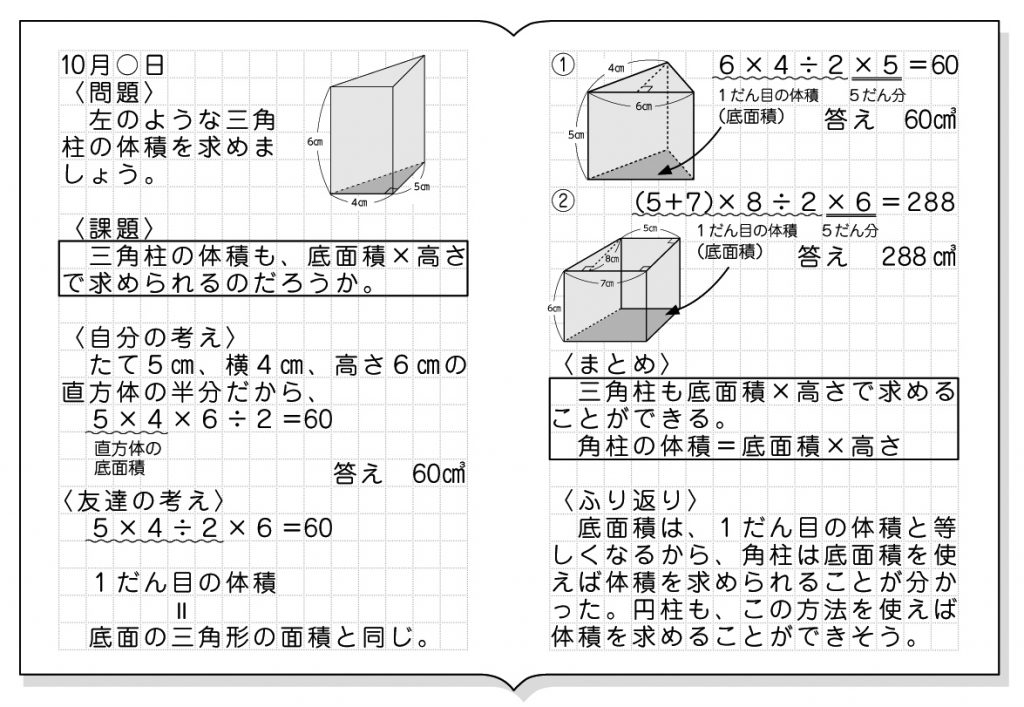立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者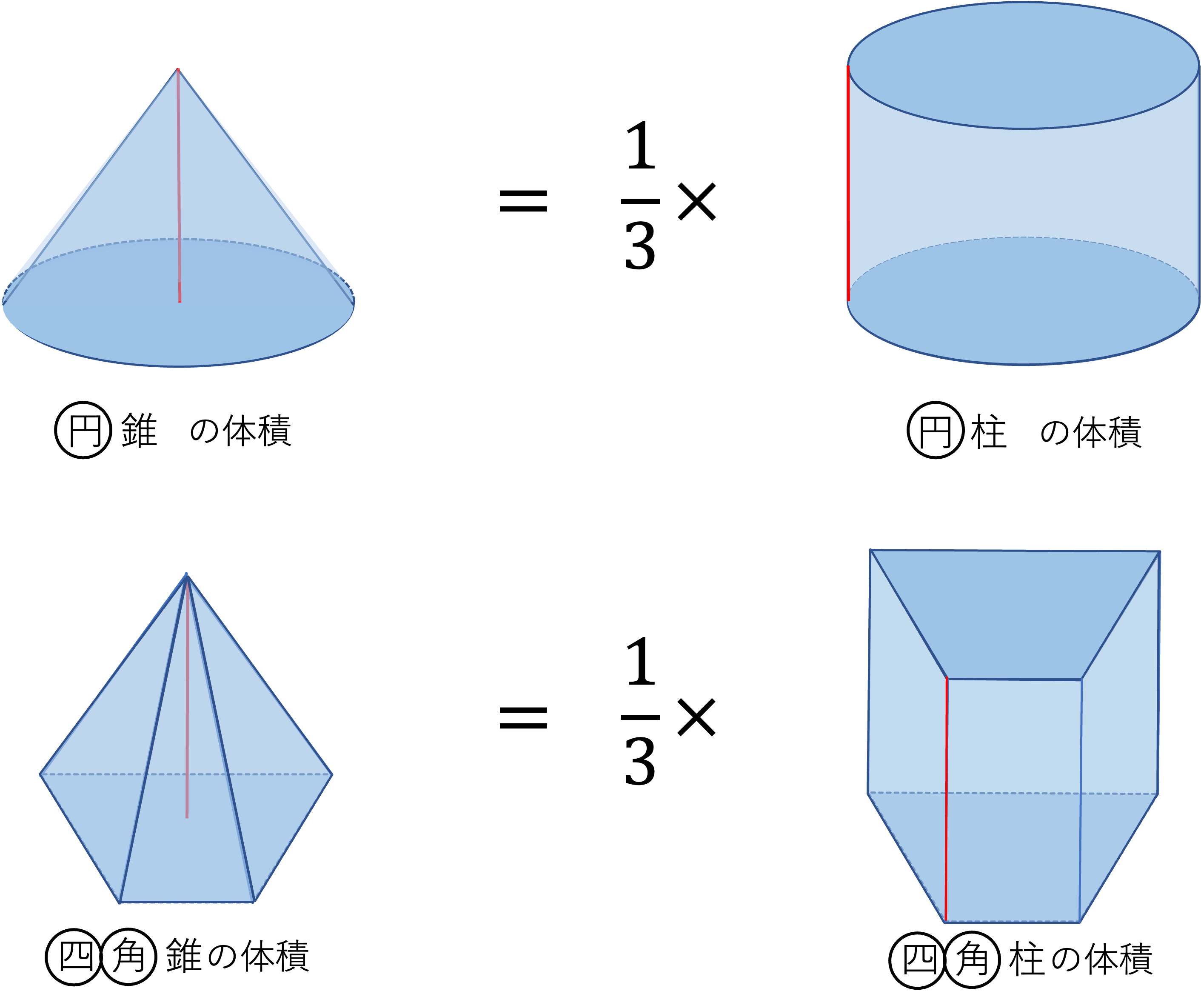
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者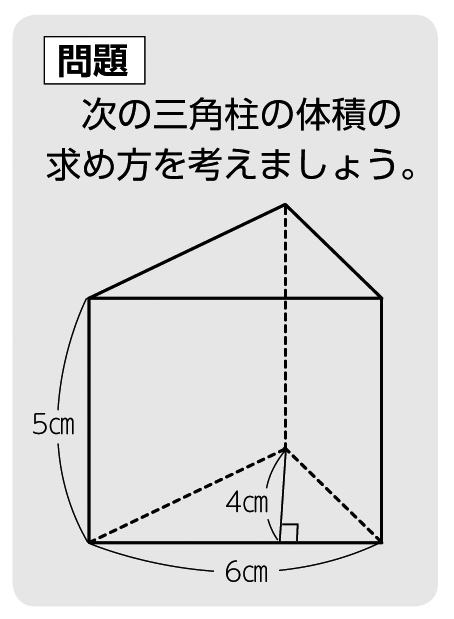
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者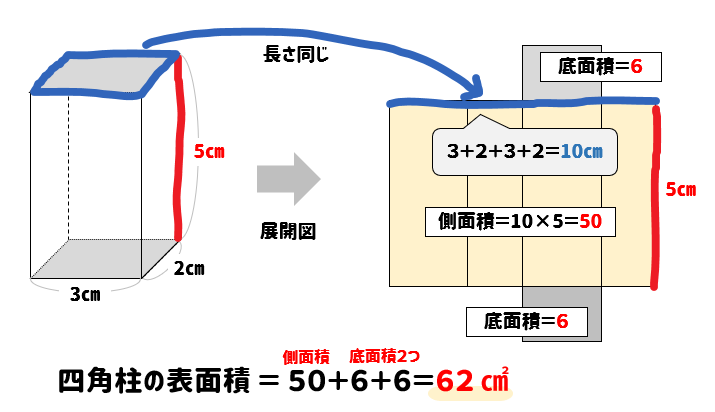
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	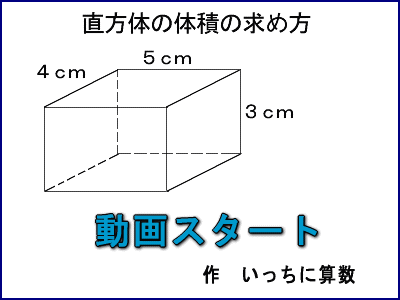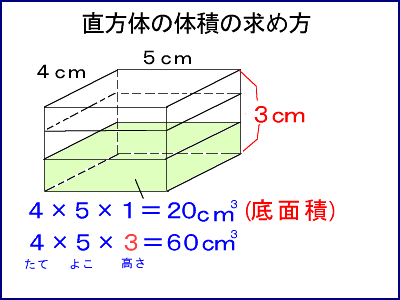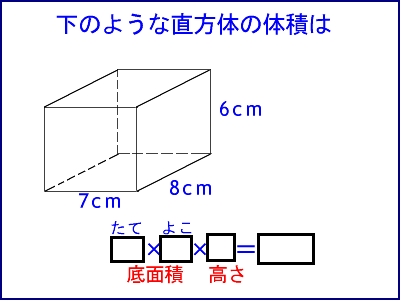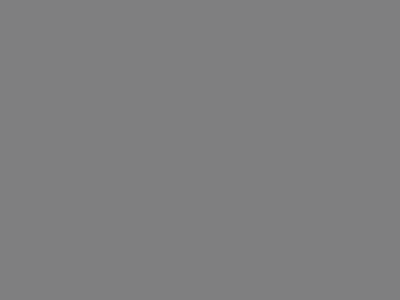立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
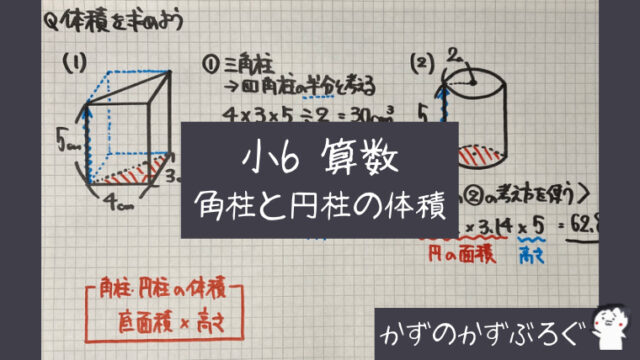立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者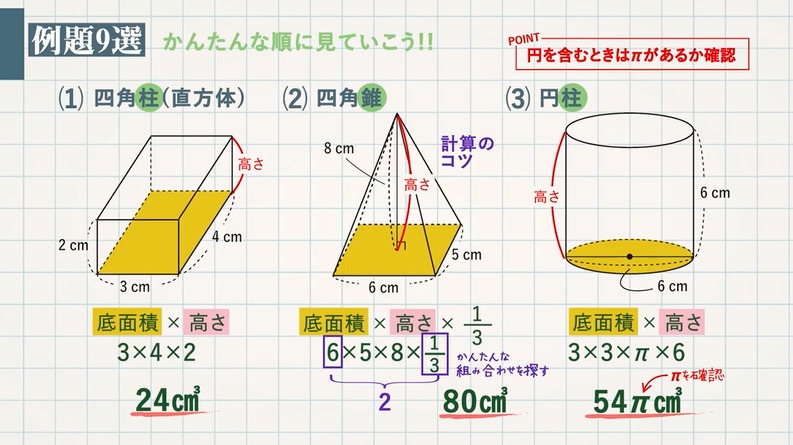
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者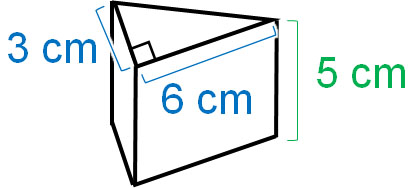
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者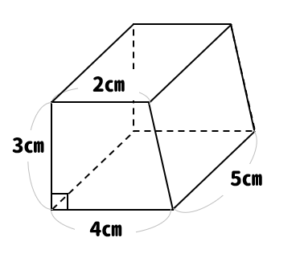
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	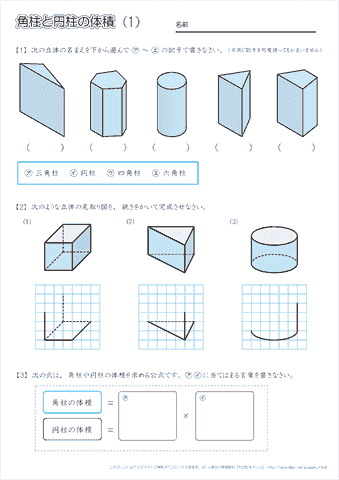立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	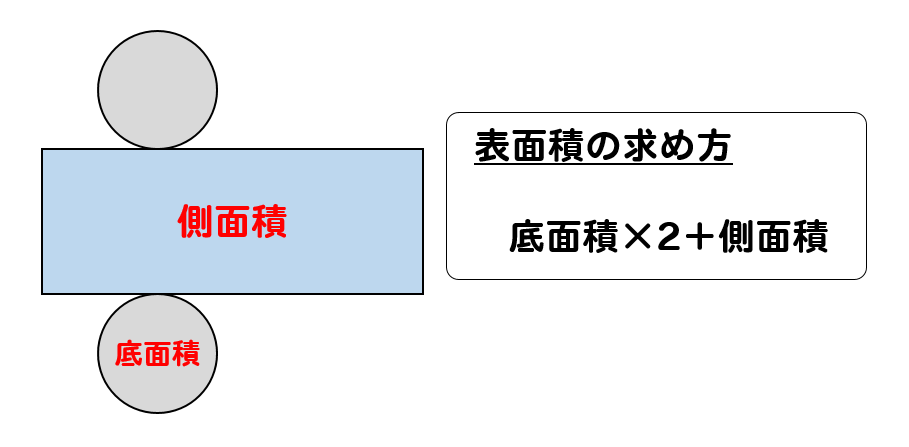立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者	立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

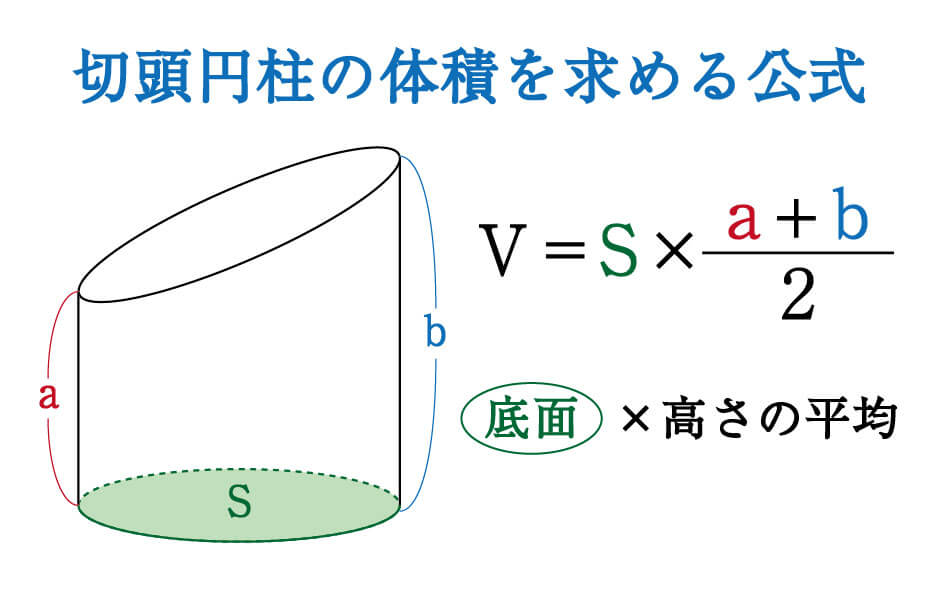
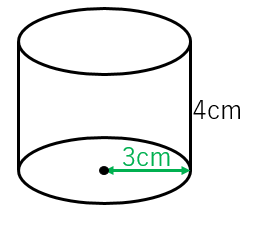
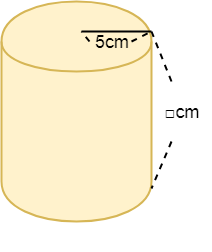
円柱の体積=底面積×高さ声に出して覚えよう 問題 下の図の円柱の底面の直径は8㎝で、高さは、10㎝です。 この円柱の体積を求めましょう。 よくある間違い その1 底面積×高さ ＝8×8×314×10 円の面積は 半径×半径×314 なので、 8cmは直径ですから >この四角柱の求め方と、体積を教えて下さい。 え？｢この四角柱の求め方｣って何ですか？ 体積は、｢底面積×高さ｣ですので、この場合は台形の面積(底面積)に高さ(この図では奥行きと言った方が分かりやすいかも知れません) 台形の面積＝(上底下底)×高さ÷2 を使うと 底面積＝(46)×2÷2＝10